Fifty Ways to Fix your Data
(Sing to the tune of “Fifty Ways to Leave Your Lover” by Paul Simon)
The problem is all about your scales, she said to me
The R-squares will be better if you’ve matched ’em mathematically
It’s just a way to make your model fit nicely
There must be fifty ways to fix your data
She said it’s really not my preference to transform
‘Cause sometimes, the new scales confuse, overfit, or misinform
But I’ll Box-Cox ’em all if it means they’ll fit the norm
There must be fifty ways to fix your data
Fifty ways to fix your data
Take the tails for a trim, Kim
Try a replace, Grace
You can use the rank, Hank
Just try ’em and see
Make it more smooth, Suz
Lots of functions you can choose
A higher degree, Dee
Will get you more fee.
In exploring a dataset, you need to be sure that you have the right numbers and that those numbers are right. You need to find and fix problems with individual data points like errors and outliers. You need to find and fix problems with observations like censored data and replicates. And you need to find and fix problems with variables like their frequency distributions and their correlations with other variables. Often, rehabilitating variables involves transformations, methods of changing the scales of your variables that might further your analyses.
As part of this process, you should consider what other information you can add that might be relevant to your analysis. This is especially important if you are planning to develop an exploratory statistical model. Experience will tell you when expanding your dataset might make a difference and when it won’t. If you don’t have that experience yet, start by learning about why you might transform variables and how it can be done. Then practice; try a variety of different techniques and learn along the way. But first you need to understand some of the pros and cons of what you might do to your dataset.
Transformations: Yes But No But Yes
There is some controversy over the use of transformations (and other methods of creating new variables) that has caused a few statisticians to argue forcefully either for or against their use. The three most common arguments that have been made against the use of transformations involve:
- Analyze what you measure. Don’t complicate the analysis unnecessarily. Stick to what the instrument was designed to measure in the way it was designed to measure it.
- Use scales consistently. Don’t confuse your readers unnecessarily. Report results in the same units that you used to measure the data.
- Let the data decide. Don’t capitalize on chance by overfitting your model. Your results should work on other samples from the same population.
There is a single simple argument for the use of transformations—they work better than the original variable scales. If they don’t work better, you don’t use them. William of Ockham would have liked that argument. So what constitutes working better? Consider these examples of the three ways that transformations are used.
One, perhaps the most important use of transformations is to reduce the effects of violations of statistical assumptions. If you plan to do any statistical analysis that involves using a Normal (or other) distribution as a model of your dependent variable, it’s important to use a scale that makes the data fit the distribution as closely as possible. If the data aren’t a good fit for the distribution, probabilities calculated for some tests and statistics will be in error. Because costly or risky decisions may be made from these probabilities, inaccuracies can be a big deal. So using a transformation to correct violations of statistical assumptions is a very important use.
Two, perhaps the most common use of transformations is to find scales that optimize the linear correlation between data for a dependent variable and data for independent variables. Statistical model building almost always benefits from this use of transformations. Everybody does it.
Three, perhaps the most overlooked use of transformations is, in a word, convenience. Sometimes transformations are used to convert measured data to more familiar units, improve computational efficiency, eliminate replicates, reduce the number of variables, and other actions that facilitate, but not necessarily improve, the analysis.
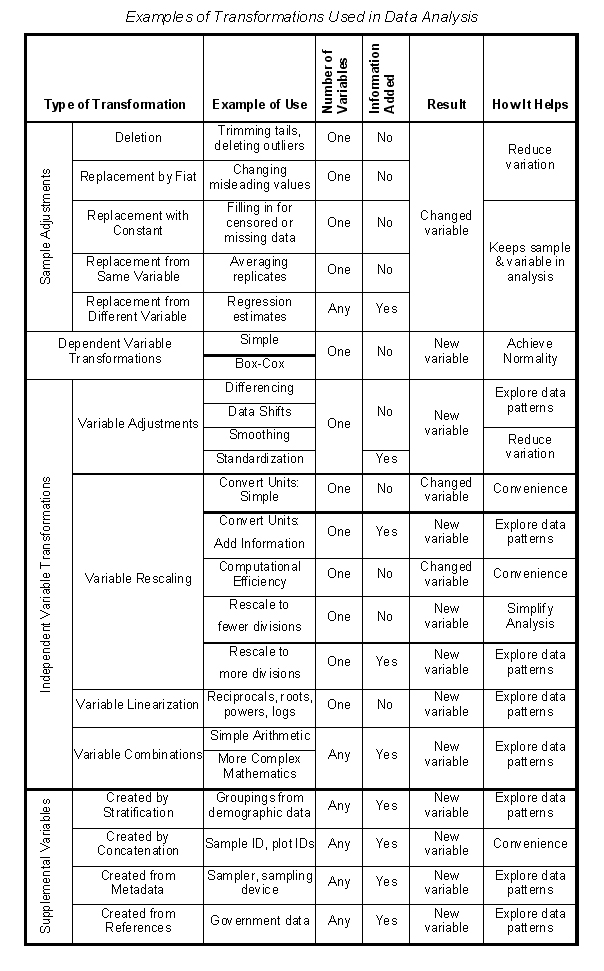
Now that you’ve been warned, here are four things you can do that might further your analyses:
- Sample Adjustments—methods for fixing missing, erroneous, or unrepresentative data points.
- Dependent Variable Transformations—methods for changing the scale of the dependent variable to minimize the effects of violations of statistical assumptions.
- Independent Variable Transformations—methods for creating new variables from the original independent variables, which have better correlations with the dependent variable.
- Supplemental Variables—methods for creating new variables from untapped data sources.
There is nothing sacred about this classification. Some of the categories might overlap or omit other ideas, so use these examples to stimulate your own thinking. In time, you’ll develop a sense of what you need for a particular analysis.
Sample Adjustments
Sample adjustments involve changing individual data points for a variable. Unlike most transformations which result in the creation of a new variable, sample adjustments leave the original variable intact. You use adjustments to correct errors, fill in missing data, reveal censored data, rein in unrepresentative replicates, and accommodate outliers. Using sample adjustments is a good place to start enhancing your data set. They are like digging out weeds and filling in holes before you plant a new lawn. It wouldn’t make sense to do it later, or worse, not at all.
Dependent Variable Transformations
After you’ve filled all the holes in your data matrix with sample adjustments, the next thing you should do is to make sure the dependent variable approximates a Normal distribution. If you haven’t looked at histograms and other indicators of Normality, always do that first. Then if your data distribution differs enough from the Normal distribution to make you nervous about your analysis, try a transformation of the dependent variable. Try several, in fact. Transformations of dependent variables create new variables but you’ll keep only one of the candidate dependent variables for an analysis. You want to pick the candidate dependent variable that fits a theoretical distribution best so that calculations of test probabilities are most accurate. If the frequency distribution of your dependent variable is skewed toward higher values, try a root transformation. If the frequency distribution is skewed toward lower values, try a power transformation. Better yet, try a Box-Cox transformation. Box-Cox transformations include the most commonly used transformations—roots, powers, reciprocals, and logs—as well as an infinite number of minor variations in between. The only downside is that the process is labor intensive if you don’t have statistical software that performs the analysis.
Independent Variable Transformations
Once you have the dependent variable you want to work with, you can go on to examine all the relationships between that dependent variable and the independent variables. While the target for transforming a dependent variable is the Normal frequency distribution, the target for transforming independent variables is a straight-line correlation between the dependent variable and each independent variable. This can be a lot of work. Remember, you have to look at correlations and plots, perhaps even for special groupings of the data. That’s the reason you always start by finding a scale for the dependent variable that fits a Normal distribution. You wouldn’t want to repeat this process for more than one dependent variable if you didn’t have to.
Variable Adjustments
Variable adjustments are changes, some quite minor, made to all the values for a variable (as opposed to just modifying specific samples as in sample adjustments). All variable adjustments create new independent variables for analysis. Examples of variable adjustments include:
- Differencing. Differencing involves subtracting the value of a variable from a subsequent value of the same variable, usually used to highlight differences. Durations in a time-series are calculated by differencing.
- Smoothing. Smoothing is the opposite of differencing and usually involves some type of averaging. Smoothing is used to suppress data noise so patterns become more evident.
- Shifting. Data shifting involves moving data up or down one or more rows in a data matrix to produce new variables called lags (when previous times are shifted to the current time) or leads (when subsequent times are shifted to the current time). Shifting all the data by one row is called a first-order lag or lead. Shifting data for a variable by k rows is called a k-order lag or lead.
- Standardizing. Standardizing involves equating the scales of some variables, usually by dividing the values by a reference value. Examples include adjusting currency for inflation, and calculating z-scores and percentages. differencing, data shifting, smoothing, and standardizing.
Variable Rescaling
Sometimes it can be useful to change the scale or units of a variable to simplify or facilitate an analysis, by:
- Rescaling for computational efficiency
- Converting units, either with or without adding information
- Converting quantitative scales to qualitative scales
- Increasing the number of scale divisions
- Decreasing the number of scale divisions
Changing the scale of a variable is different from changing the units of a variable. Both are important. Changing units usually involves only simple mathematical calculations with or without the addition or deletion of information. Rescaling variables involves adding or removing information or changing a point of reference. Rescaling usually involves making changes based on logic but may include mathematical calculations as well. Recoding is perhaps the most common way of rescaling a variable. Some statistical software have utilities to facilitate recoding.
Variable Linearization
Improving the correlation between a dependent variable and an independent variable is a big part of statistical modeling. The objectives of this type of transformation are (1) to persuade the data to follow a straight line, and (2) minimize the scatter of the data around the line. Here are a few examples of mathematical functions used as transformations.
Variable Combinations
Variable combinations are new variables created from two or more existing variables using simple arithmetic operations (sums, differences, products, and ratios) or more complex mathematical functions. Variable combinations should be based on theory rather than created for convenience. Usually the variables combined should have the same units (e.g., dollars), although units can be standardized using z-scores.
Supplemental Variables
You won’t necessarily just add variables at the beginning of your analysis. You may add them continuously throughout your analysis as you learn more about your data. Some variables may turn out to be critical to the analysis and others will just facilitate reporting or some other ancillary function. Supplemental variables can be creating by concatenating or partitioning existing variables, or by adding new information from metadata or external references (e.g., federal census data).
You Can Teach Old Data New Tricks
When your instructor gave you a dataset in Statistics 101, that was it. You did what the assignment called for, got the desired answer, and you were finished. But it doesn’t work that way in the real world overflowing with data but lacking in wisdom. Sometimes you have to put more effort into making sense of things. Statistics is the mortar that brings data and metadata together to make building blocks of information into a temple of wisdom. Transformations are like mason’s tools. They can smooth, reshape, adjust, add texture, augment, condense, and on and on. Suffice it to say that with transformations, there must be at least fifty ways to fix your data.
Read more about using statistics at the Stats with Cats blog. Join other fans at the Stats with Cats Facebook group and the Stats with Cats Facebook page. Order Stats with Cats: The Domesticated Guide to Statistics, Models, Graphs, and Other Breeds of Data Analysis at Wheatmark, amazon.com, barnesandnoble.com, or other online booksellers.







Good day I was fortunate to approach your Topics in google
your Topics is excellent
I obtain a lot in your Topics really thank your very much
btw the theme of you website is really terrific
where can find it
I post a blog every Sunday at https://statswithcats.wordpress.com/. Most of the blogs are excerpts from a book, Stats with Cats, that I will be publishing later this year.
Pingback: Secrets of Good Correlations | Stats With Cats Blog
Find and pick some good things from you and it helps me to solve a problem, thanks.
– Henry
http://www.rachatdecredit.net/rachat-de-credit-personnel-quels-sont-les-avantages.html
Pingback: You’re Off to Be a Wizard | Stats With Cats Blog
I love browsing your blog because you can always get us fresh and cool stuff, I feel that I ought to at least say a thank you for your hard work.
– Henry
Thank you!
Pingback: The Data Dozen | Stats With Cats Blog
Pingback: Ten Tactics used in the War on Error | Stats With Cats Blog
Pingback: Regression Fantasies: Part II | Stats With Cats Blog
Pingback: Regression Fantasies: Part III | Stats With Cats Blog
Pingback: Homepage
There is noticeably a bundle to know about this. I assume you created certain good points in capabilities also 530449
Pingback: The Best Super Power of All | Stats With Cats Blog
Pingback: The Foundation of Professional Graphs | Stats With Cats Blog
Pingback: HOW TO WRITE DATA ANALYSIS REPORTS. LESSON 1—KNOW YOUR CONTENT. | Stats With Cats Blog
Pingback: A helpful Stats website | Academic murmuring
Pingback: Why You Don’t Always Get the Correlation You Expect | Stats With Cats Blog
Can I simply just say what a relief to discover somebody
who genuinely understands what they’re discussing
on the net. You definitely understand how to bring a problem to light and make it important.
A lot more people have to check this out and understand this side of the
story. I was surprised that you’re not more popular since you definitely
possess the gift.
Love this particular page as it was helpful! and Funny!! cheers
Pingback: Ten Ways Statistical Models Can Break Your Heart | Stats With Cats Blog
Pingback: How to Write Data Analysis Reports in Six Easy Lessons | Stats With Cats Blog
Pingback: Regression Fantasies | Stats With Cats Blog
Pingback: Searching for Answers | Stats With Cats Blog
Pingback: Stats With Cats Blog
Pingback: Catalog of Models | Stats With Cats Blog
Perfect…Thank You !!!
Pingback: Dare to Compare – Part 2 | Stats With Cats Blog
Pingback: How to write data analysis reports. Lesson 1—Know Your Content. – Big Data Made Simple – One source. Many perspectives.
Pingback: What to Look for in Data – Part 2 | Stats With Cats Blog
Pingback: 35 Ways Data Go Bad | Stats With Cats Blog