Nine patterns of three types of relationships that aren’t spurious.
When analysts see a large correlation coefficient, they begin speculating about possible reasons. They’ll naturally gravitate toward their initial hypothesis (or preconceived notion) which set them to investigate the data relationship in the first place. Because hypotheses are commonly about causation, they often begin with this least likely type of relationship using the most simplistic of relationship pattern, a direct one-event-causes-another.
A topology of data relationships is important because it helps people to understand that not all relationships reflect a cause. They may just be the result of an influence or an association or even mere coincidence. Furthermore, you can’t always tell what type and pattern of relationship a data set represents. There are at least 27 possibilities not even counting spurious relationships. That’s where numbercrunching ends and statistical-thinking shifts into high-gear. Be prepared.
Types of Data Relationships
Besides causation, relationships can also reflect influence or association.
Causes
A cause is a condition or event that directly triggers, initiates, makes happen, or brings into being another condition or event. A cause is a sine qua non; without a cause a consequent will not occur. Causes are directional. A cause must precede its consequent.
Influences
An influence is a condition or event that changes the manifestation of an existing condition or event. Influences can be direct or mediated by a separate condition or event. Influences may exist at any time before or after the influenced condition or event. Influences may be unidirectional or bidirectional.
Associations
Associations are two conditions or events that appear to change in a related way. Any two variables that change in a similar way will appear to be associated. Thus, associations can be spurious or real. Associations may exist at any time before or after the associated condition or event. Unlike causes and influences, associated variables have no effect on each other and may not exist in different populations or in the same population at different times or places.
Associations are commonplace. Most observed correlations are probably just associations. Influences and causes are less common but, unlike associations, they can be supported by the science or other principles on which the data are based. The strength of a correlation coefficient is not related to the type of relationship. Causes, influences, and associations can all have strong as well as weak correlations depending on the efficiency of the variables being correlated and the pattern of the relationship.

Patterns of Data Relationships
Direct relationships are easy to understand and, if there are no statistical obfuscations, should exhibit a high degree of correlation. In practice, though, not every relationship is direct or simple. Some are downright complex.
Here are nine relationships that I could think of. There may be more. These relationships involve events or conditions termed A, B, and C.

Direct Relationship
Most discussions of correlation and causation focus on the simple, direct relationship that one event or condition, A, is related to a second event or condition, B. The relationship proceeds in only one direction. For example, gravitational forces from the Moon and Sun cause ocean tides on the Earth. A causes B but B does not cause A. Another direct relationship is that age influences height and weight. Age doesn’t cause height and weight but we tend to grow larger as we age so A influences B. B does not influence A.

Feedback Relationship
In a feedback relationship, A and B are linked in a loop. A causes or influences B, which then causes or influences A, and so on. Feedback relationships are bidirectional. They will be correlated. For example, poor performance in school or at work (A) creates stress (B) which degrades performance further (A) leading to more stress (B) and so on.

Common-Cause Relationship
In a common-cause relationship, a third event or condition, C, causes or influences both A and B. For example, hot weather © causes people to wear shorts (A) and drink cool beverages (B). Wearing shorts (A) doesn’t cause or influence beverage consumption (B), although the two are associated by their common cause. A plot of this data will show that A and B are correlated, but the correlation represents an underlying association rather than an influence or a cause. Another example is the influence obesity has on susceptibility to a variety of health maladies.
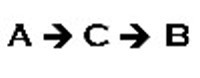
Mediated Relationship
In a mediated relationship, A causes or influences C and C causes or influences B so that it appears that A causes B. A and B will be correlated. For example, rainy weather (A) often induces people to go to their local shopping mall for something to do ©. While there, they shop, eat lunch, and go to the movies or other entertainment venues thus providing the mall with increased revenues (B). In contrast, snowstorms (A) often induce people to stay at home © thus decreasing mall revenues (B). Bad weather doesn’t cause or influence mall revenues directly but does influence whether people visit the mall.

Stimulated Relationship
In a stimulated relationship, A causes or influences B but only in the presence of C. Stimulated relationships may not appear to be correlated using a Pearson correlation coefficient but may using a partial correlation. There are many examples of this pattern, such as metabolic and chemical reactions involving enzymes or catalysts.
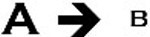
Suppressed Relationship
In a suppressed relationship, A causes or influences B but not in the presence of C. As with stimulated relationships, suppressed relationships may only appear to be correlated using a partial correlation coefficient. Medicine has many examples of suppressed and stimulated relationships. For example, pathogens (A) cause infections (B) but not in the presence of antibiotics (C). Some drugs (A) cause side effects (B) only in certain at-risk populations (C).

Inverse Relationship
In inverse relationships, the absence of A causes or influences B, OR the presence of A minimizes B. Correlation coefficients for inverse relationships are negative. For example, vitamin deficiencies (A) cause or influence a wide variety of symptoms (B).

Threshold Relationship
In threshold relationships, A causes or influences B only when A is above a certain level. For example, rain (A) causes flooding (B) only when the volume or intensity is very high. These relationships aren’t usually revealed by correlation coefficients.

Complex Relationship
In complex relationships, many A factors or events contribute to the cause or influence of B. Numerous environmental processes fit this pattern. For example, A variety of atmospheric and astronomical factors (A) contribute to influencing climate change (B). Even many correlation coefficients may not explain this type of relationship; it takes more involved statistical analyses.

Spurious Data Relationships
There are also a variety of spurious relationships in which A appears to cause or influence B, but does not. Often the reason is that the relationship is based on anecdotal evidence that is not valid more generally. Sometimes spurious relationships may be some other kind of relationship that isn’t understood. Here are five other reasons why spurious relationships are so common.
Misunderstood relationships
The science behind a relationship may not be understood correctly. For example, doctors used to think that spicy foods and stress caused ulcers. Now, there is greater recognition of the role of bacterial infection. Likewise, hormones have been found to be the leading cause of acne rather than diet (i.e., consumption of chocolate and fried foods).
Misinterpreted statistics
There are many examples of statistical relationships being interpreted incorrectly. For example, the sizes of homeless populations appear to influence crime. Then again, so do the numbers of museums and the availability of public transportation. All of these factors are associated with urban areas, but not necessarily crime.
Misinterpreted observations
Incorrect reasons are attached to real observations. Many old wives tales are based on credible observations. For example, the notion that hair and nails continue to grow after death is an incorrect explanation for the legitimate observation.
Urban legends
Some urban legends have a basis in truth and some are pure fabrications, but they all involve spurious relationships. For example, In South Korea, it is believed that sleeping with a fan in a closed room will result in death.
Biased Assertions
Some spurious relationships are not based on any evidence, but instead, are claimed in an attempt to persuade others of their validity. For example, the claim that masturbation makes you have hairy palms is not only ludicrous but also easily refutable. Likewise, almost any advertisement in support of a candidate in an election contains some sort of bias, such as cherry picking.
Coincidences
Mother Nature has a wicked sense of humor. Don’t believe every correlation coefficient you calculate.








